#MT02 - Come Claude Shannon inventò il futuro
L'odierna era dell'informazione è possibile solo grazie all'opera pionieristica di un genio solitario.
Questo è il secondo di una serie di articoli che ci accompagneranno, durante una breve gita nella “tana del coniglio” matematico, alla scoperta di un argomento che tange - come molti altri - lo studio di #bitcoin: lo scambio di informazioni crittografate.
Traduzione dall’originale di David Tse - Pubblicato il 22 dic 2020
La scienza cerca le leggi fondamentali della natura. La matematica cerca nuovi teoremi per costruire su quelli vecchi. L'ingegneria costruisce sistemi per risolvere i bisogni umani. Le tre discipline sono interdipendenti ma distinte. Molto raramente un individuo fornisce contemporaneamente contributi fondamentali a tutte e tre, ma Claude Shannon era un individuo raro.
Nonostante sia il soggetto del recente documentario "The Bit Player" e il suo lavoro e la sua filosofia di ricerca abbiano ispirato la mia carriera, Shannon non è esattamente un nome conosciuto. Non ha mai vinto un premio Nobel e non è stato una celebrità come Albert Einstein o Richard Feynman, né prima né dopo la sua morte nel 2001. Ma più di 70 anni fa, con un singolo articolo rivoluzionario, ha gettato le basi dell'intera infrastruttura di comunicazione alla base della moderna era dell'informazione.
Shannon è nato a Gaylord, nel Michigan, nel 1916, figlio di un uomo d'affari locale e di un'insegnante. Dopo essersi laureato in ingegneria elettrica e matematica all'Università del Michigan, scrisse una tesi di master al Massachusetts Institute of Technology che applicava una disciplina matematica chiamata algebra booleana all'analisi e alla sintesi dei circuiti di commutazione. Si trattò di un lavoro trasformativo, che trasformò la progettazione dei circuiti da un'arte a una scienza e che oggi è considerato il punto di partenza della progettazione dei circuiti digitali.
La comunicazione è uno dei bisogni fondamentali dell'uomo. Dai segnali di fumo ai piccioni viaggiatori, dal telefono alla televisione, gli esseri umani hanno sempre cercato metodi che permettessero loro di comunicare più lontano, più velocemente e in modo più affidabile. Ma l'ingegneria dei sistemi di comunicazione è sempre stata legata alla fonte specifica e al mezzo fisico. Shannon si chiese invece: "Esiste una grande teoria unificata per la comunicazione?". In una lettera del 1939 al suo mentore, Vannevar Bush, Shannon delineò alcune delle sue idee iniziali sulle "proprietà fondamentali dei sistemi generali per la trasmissione dell'intelligenza". Dopo aver lavorato al problema per un decennio, Shannon pubblicò finalmente il suo capolavoro nel 1948: "Una teoria matematica della comunicazione".
Il cuore della sua teoria è un modello semplice ma molto generale di comunicazione: Un trasmettitore codifica le informazioni in un segnale, che viene corrotto dal rumore e poi decodificato dal ricevitore. Nonostante la sua semplicità, il modello di Shannon incorpora due intuizioni chiave: isolare le fonti di informazione e di rumore dal sistema di comunicazione da progettare e modellare entrambe le fonti in modo probabilistico. Shannon immaginava che la fonte di informazione generasse uno dei tanti possibili messaggi da comunicare, ognuno dei quali aveva una certa probabilità. Il rumore probabilistico aggiungeva ulteriore casualità che il ricevitore doveva districare.
Prima di Shannon, il problema della comunicazione era visto principalmente come un problema di ricostruzione deterministica del segnale: come trasformare un segnale ricevuto, distorto dal mezzo fisico, per ricostruire l'originale nel modo più accurato possibile. Il genio di Shannon risiede nella sua osservazione che la chiave della comunicazione è l'incertezza. Dopotutto, se sapeste in anticipo cosa vi dirò in questa rubrica, che senso avrebbe scriverla?
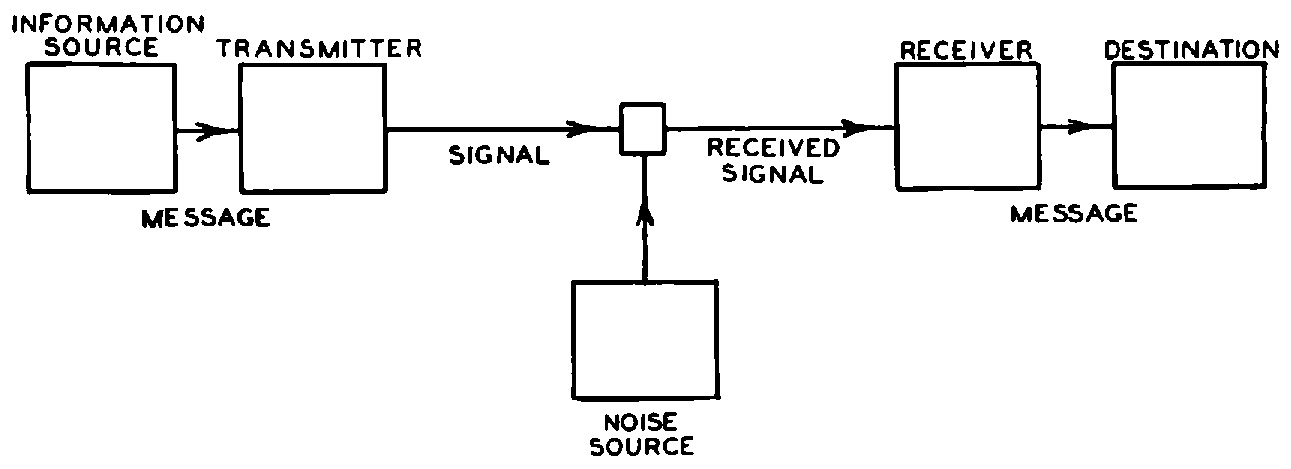
Questa singola osservazione spostò il problema della comunicazione dall'ambito fisico a quello astratto, consentendo a Shannon di modellare l'incertezza utilizzando la probabilità. Questo fu uno shock totale per gli ingegneri della comunicazione dell'epoca.
Dato questo quadro di incertezza e probabilità, Shannon si propose, nel suo storico articolo, di determinare sistematicamente il limite fondamentale della comunicazione. La sua risposta si articola in tre parti. Il concetto di "bit" di informazione, utilizzato da Shannon come unità di base dell'incertezza, svolge un ruolo centrale in tutte e tre le parti. Un bit può essere sia un 1 che uno 0, e il documento di Shannon è il primo a usare questa parola (anche se il matematico John Tukey l'ha usata per primo in una nota).
In primo luogo, Shannon elaborò una formula per il numero minimo di bit al secondo per rappresentare l'informazione, un numero che chiamò tasso di entropia, H. Questo numero quantifica l'incertezza che comporta la determinazione del messaggio che la sorgente genererà. Più basso è il tasso di entropia, minore è l'incertezza e quindi più facile è comprimere il messaggio in qualcosa di più breve. Ad esempio, inviare un SMS al ritmo di 100 lettere inglesi al minuto significa inviare uno dei 26100 messaggi possibili ogni minuto, ciascuno rappresentato da una sequenza di 100 lettere. Si potrebbero codificare tutte queste possibilità in 470 bit, dato che 2470 ≈ 26100. Se le sequenze fossero ugualmente probabili, la formula di Shannon direbbe che il tasso di entropia è effettivamente di 470 bit al minuto. In realtà, alcune sequenze sono molto più probabili di altre e il tasso di entropia è molto più basso, consentendo una maggiore compressione.
In secondo luogo, fornì una formula per il numero massimo di bit al secondo che possono essere comunicati in modo affidabile in presenza di rumore, che chiamò capacità del sistema, C. Questa è la velocità massima con cui il ricevitore può risolvere l'incertezza del messaggio, rendendola di fatto il limite di velocità della comunicazione.
Infine, dimostrò che una comunicazione affidabile dell'informazione dalla fonte in presenza di rumore è possibile se e solo se H < C. Quindi, l'informazione è come l'acqua: Se la portata è inferiore alla capacità del tubo, il flusso passa in modo affidabile.
Sebbene si tratti di una teoria della comunicazione, è allo stesso tempo una teoria di come l'informazione viene prodotta e trasferita - una teoria dell'informazione. Per questo Shannon è oggi considerato "il padre della teoria dell'informazione".
I suoi teoremi hanno portato a conclusioni controintuitive. Supponiamo di parlare in un luogo molto rumoroso. Qual è il modo migliore per assicurarsi che il messaggio arrivi? Forse ripeterlo molte volte? Questo è certamente il primo istinto di chiunque in un ristorante rumoroso, ma si scopre che non è molto efficiente. Certo, più volte ci si ripete, più la comunicazione è affidabile. Ma si sacrifica la velocità per l'affidabilità. Shannon ci ha mostrato che possiamo fare molto meglio. La ripetizione di un messaggio è un esempio di utilizzo di un codice per trasmettere un messaggio e, utilizzando codici diversi e più sofisticati, si può comunicare velocemente - fino al limite di velocità, C - mantenendo un determinato grado di affidabilità.
Un'altra conclusione inaspettata che deriva dalla teoria di Shannon è che qualunque sia la natura dell'informazione - sia essa un sonetto di Shakespeare, una registrazione della Quinta Sinfonia di Beethoven o un film di Kurosawa - è sempre più efficiente codificarla in bit prima di trasmetterla. Così, ad esempio, in un sistema radiofonico, anche se sia il suono iniziale che il segnale elettromagnetico inviato via etere sono forme d'onda analogiche, i teoremi di Shannon implicano che è ottimale digitalizzare prima l'onda sonora in bit e poi mappare questi bit nell'onda elettromagnetica. Questo sorprendente risultato è una pietra miliare della moderna era dell'informazione digitale, dove il bit regna sovrano come moneta universale dell'informazione.
La teoria generale della comunicazione di Shannon è così naturale che è come se avesse scoperto le leggi della comunicazione dell'universo, invece di inventarle. La sua teoria è fondamentale come le leggi fisiche della natura. In questo senso, era uno scienziato.
Shannon ha inventato una nuova matematica per descrivere le leggi della comunicazione. Ha introdotto nuove idee, come il tasso di entropia di un modello probabilistico, che sono state applicate in rami della matematica molto ampi, come la teoria ergodica, lo studio del comportamento a lungo termine dei sistemi dinamici. In questo senso, Shannon era un matematico.
Ma soprattutto Shannon era un ingegnere. La sua teoria era motivata da problemi pratici di ingegneria. E mentre era esoterica per gli ingegneri del suo tempo, la teoria di Shannon è diventata oggi il quadro standard alla base di tutti i sistemi di comunicazione moderni: ottici, subacquei, persino interplanetari. Personalmente, ho avuto la fortuna di partecipare a uno sforzo mondiale per applicare e ampliare la teoria di Shannon alle comunicazioni wireless, aumentando la velocità di comunicazione di due ordini di grandezza su più generazioni di standard. In effetti, lo standard 5G attualmente in fase di lancio utilizza non uno ma due codici pratici dimostrati per raggiungere il limite di velocità di Shannon.

Shannon ha trovato le basi per tutto questo più di 70 anni fa. Come ci riuscì? Concentrandosi senza sosta sulla caratteristica essenziale di un problema, ignorando tutti gli altri aspetti. La semplicità del suo modello di comunicazione è una buona illustrazione di questo stile. Sapeva anche concentrarsi su ciò che è possibile, piuttosto che su ciò che è immediatamente pratico.
Il lavoro di Shannon illustra il vero ruolo della scienza di alto livello. Quando ho iniziato la scuola di specializzazione, il mio consulente mi disse che il lavoro migliore avrebbe potato l'albero della conoscenza, piuttosto che farlo crescere. Allora non sapevo cosa pensare di questo messaggio; ho sempre pensato che il mio compito di ricercatore fosse quello di aggiungere i miei ramoscelli. Ma nel corso della mia carriera, quando ho avuto l'opportunità di applicare questa filosofia nel mio lavoro, ho cominciato a capire.
Quando Shannon iniziò a studiare la comunicazione, gli ingegneri disponevano già di una vasta collezione di tecniche. È stato il suo lavoro di unificazione che ha potato tutti questi ramoscelli di conoscenza in un unico albero coerente e bello, che ha dato i suoi frutti a generazioni di scienziati, matematici e ingegneri.
Come acquistare Bitcoin?
Personalmente, reputo il miglior servizio quello offerto da Relai.
Per acquistare bitcoin risparmiando lo 0,5% in commissioni puoi usare il codice “REL3166”.
Si tratta di un’applicazione sviluppata da un’azienda svizzera che applica una politica di KYC light: a differenza dei grandi exchange non richiede registrazioni o dati personali, tutto ciò che serve per acquistare è il tuo IBAN.
E’ lo strumento ottimale per impostare dei piani di accumulo (DCA).
Per ridurre al massimo le commissioni di acquisto, ti consiglio di:
effettuare acquisti maggiori di 100€ (-0,5%)
impostare un piano di accumulo settimanale o mensile (-0,5%)
applicare il codice invito REL3166 (-0,5%)
Una delle migliori caratteristiche è il servizio non-custodial. Gli euro bonificati a Relai vengono convertiti automaticamente in bitcoin e trasferiti su un wallet di cui sei solo tu ad avere il controllo. I grossi exchange, al contrario, non forniscono le chiavi private ai clienti. In più Relai non vende centinaia di inutili criptovalute, ma solo bitcoin.
Cosa ci guadagno? Quello che fanno guadagnare i referral code. In questo caso se acquisti usando il codice “REL3166” risparmi lo 0,5% sulle commissioni e io ricevo (in bitcoin) lo 0,5% dell’importo che hai deciso di investire.
Per ulteriori informazioni, o per effettuare il primo acquisto, premi sul pulsante sottostante e ti verrà mostrata una dettagliata guida in italiano.
NOTA - Questo NON è un messaggio pubblicitario. Relai è un servizio che utilizzo personalmente e che reputo tra i migliori sul mercato in termini di affidabilità, sicurezza e facilità d’uso. Lo consiglio spesso ad amici e parenti.





